Im zweiten Teil dieses Artikels geht es um besondere Aspekte, die im praktischen Umgang mit FFT Messungen hilfreich sind. FFT Messungen finden Anwendung in zahlreichen Applikationen. Die Darstellung der Resultate erfolgt meist als Graph und ist einfach zu interpretieren. Es gibt jedoch einige notwendige Voraussetzungen, die für eine korrekte und genaue FFT Messung notwendig sind. Dieser Artikel gibt wertvolle Tipps dafür.
Wie im ersten Teil ausgeführt, bilden die Abtastrate fs des Messsystems und die Blocklänge BL die beiden zentralen Parameter einer FFT. Die Abtastrate besagt, wie häufig das zu analysierende analoge Signal abgetastet wird. Bei der Aufnahme von wav-Dateien über eine handelsübliche PC-Soundkarte wird das Audiosignal üblicherweise 44100 Mal pro Sekunde abgetastet.
Nyquist Theorem
Harry Nyquist war der Entdecker einer fundamentalen Regel bei der Abtastung von analogen Signalen: Die Abtastfrequenz muss mindestens dem Doppelten der oberen interessierenden Signalfrequenz entsprechen. Soll beispielsweise ein Signal abgetastet werden, das Frequenzen bis 24 kHz enthält, so ist dafür mindestens eine Abtastrate von 48 kHz erforderlich. Die halbe Abtastrate wird hierbei „Nyquist-Frequenz“ genannt.
Was geschieht aber, wenn dem System Signalanteile oberhalb der Nyquist-Frequenz zugeführt werden?
Aliasing
In der Regel wird eine Signalperiode (also ein Sinus-Wellenzug) mit ausreichend vielen Abtastwerten („Samples“) abgetastet. Bei einem 6 kHz Signal mit 48 kHz Abtastrate sind dies zum Beispiel noch 8 Samples. Bei 12 kHz stehen nur noch 4 Samples zur Verfügung. Bei der Nyquist-Frequenz lediglich 2 Samples. Mit 2 Samples oder mehr ist es möglich, das Signal verlustfrei wieder zu rekonstruieren. Stehen jedoch weniger als 2 Samples zur Verfügung, so entstehen Signalanteile, die im abgetasteten (ursprünglichen) Signal gar nicht vorkommen.
Spiegel-Frequenzen
In der FFT zeigen sich diese Signale als Spiegelfrequenzen. Wird die Nyquist-Frequenz überschritten, spiegelt sich das Signal an dieser imaginären Grenze und fällt in das Nutz-Frequenzband zurück. Das folgende Video zeigt ein FFT System mit 44.1 kHz Abtastrate. Diesem System wird ein Sweep-Signal von 15 kHz bis 25 kHz zugeführt.
Diesen unerwünschten Spiegelfrequenzen wird durch ein analoges Tiefpassfilter vor der Abtastung entgegengewirkt (Anti-Aliasing Filter). Das Filter stellt sicher, dass Frequenzen oberhalb der Nyquist-Frequenz unterdrückt werden.
Zeitfensterung
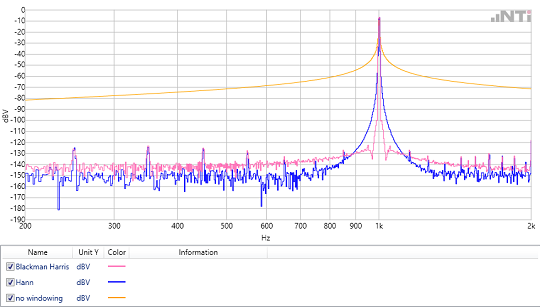
Die Zeitfensterung dient bei periodisch fortgesetzten Signalen dazu, die unerwünschten Übergangsprünge am Ende der Abtastung zu glätten. (siehe Teil 1) Damit werden Verschmierungen im Spektrum verhindert. Es gibt zahlreiche Fenster-Arten, die sich zum Teil nur durch Nuancen unterscheiden. Bei der Auswahl des Zeitfensters gilt folgende Grundregel: Jedes Fenster bedingt einen Kompromiss zwischen Frequenz-Selektivität und Amplitudengenauigkeit.
Mittelung von Spektren
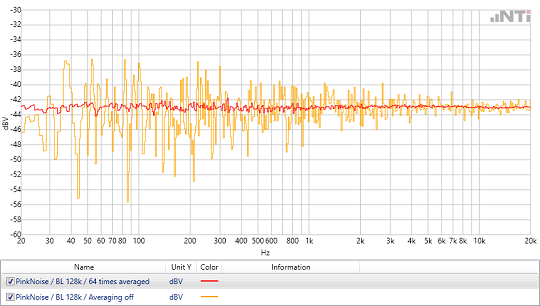
Bei der Analyse nichtperiodischer Signale, wie z.B. Rauschen oder Musik, ist es oft von Vorteil, mehrere FFT Blöcke zu erfassen und daraus Mittelwerte zu bestimmen. Dabei gibt es zwei mögliche Vorgehensweisen:
- Die klassische Mittelung: Hier werden eine Anzahl von FFTs gemessen. Jedes Resultat fliesst zu gleichen Teilen in das gemittelte Endresultat ein. Diese Methode eignet sich bei Messungen mit einer definierten Dauer.
- Die exponentielle Mittelung: Hier werden kontinuierlich FFTs gemessen. Auch hier fliessen eine feste Anzahl Resultate der kontinuierlichen Messungen in die Mittelung. Die Gewichtung erfolgt jedoch umgekehrt proportional zum ‚Alter‘ des Resultats. Die älteste der Messungen wird am wenigsten berücksichtigt, die aktuellste Messung trägt am stärksten zum gemittelten Resultat bei. Die exponentielle Mittelung wird verwendet, wenn das Spektrum über einen längeren Zeitraum kontinuierlich betrachtet wird.
Power vs. Peak Detektor
Moderne hochauflösende FFT Analysatoren bieten die Möglichkeit, die Anzahl der Messresultate von der FFT Blocklänge zu entkoppeln. Dies bringt eine Beschleunigung der Messung, insbesondere bei hochauflösenden FFTs. So müssen z.B. bei einer 2MB Blocklänge nicht mehr > 1Million Messpunkte (Bins) verarbeitet und dargestellt werden, sondern nur noch die für die Anzeige notwendige Anzahl, z.B. 1024.
Diese Zusammenfassung von FFT Bins kann auf zwei Arten geschehen:
- „MaxPeak“: Hier wird der maximale Wert der zusammengefassten FFT Resultate verwendet. Diese Art eignet sich gut für die visuelle Darstellung von FFTs
- „Power“: Hier werden die FFT Resultate energetisch summiert. Dies ist dann notwendig wenn die FFT für Berechnungen verwendet werden.
Berechnungen mit FFT Resultaten
FFTs werden überwiegend zur Visualisierung von Signalen verwendet. Es gibt jedoch auch Anwendungen, bei denen FFT Resultate verrechnet werden. So können zum Beispiel sehr einfach Pegel von definierten Frequenzbändern errechnet werden, indem diese über einen RSS (Root Sum Square) Algorithmus addiert werden.
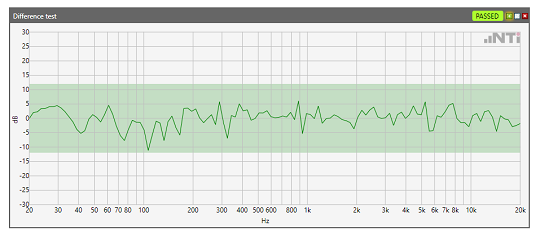
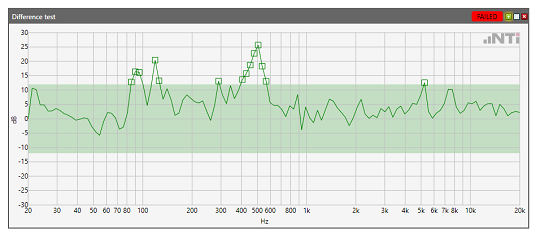
Eine weitere Anwendung ist die Differenzbildung von Spektren. Das untenstehende Beispiel zeigt eine akustische Messung eines Akkuschraubers. Das gemessene Spektrum wird von einem einmal definierten Referenzspektrum subtrahiert. Diese Differenz wird gegen eine obere und untere Toleranz verglichen. Das obere Spektrum zeigt einen intakten Akkuschrauber. Im unteren Beispiel ist das Getriebe des Prüflings defekt.
Mehr zu FFT-Messlösungen:
FX100 Audio Analysator XL2 Audio- und Akustik-Analysator